
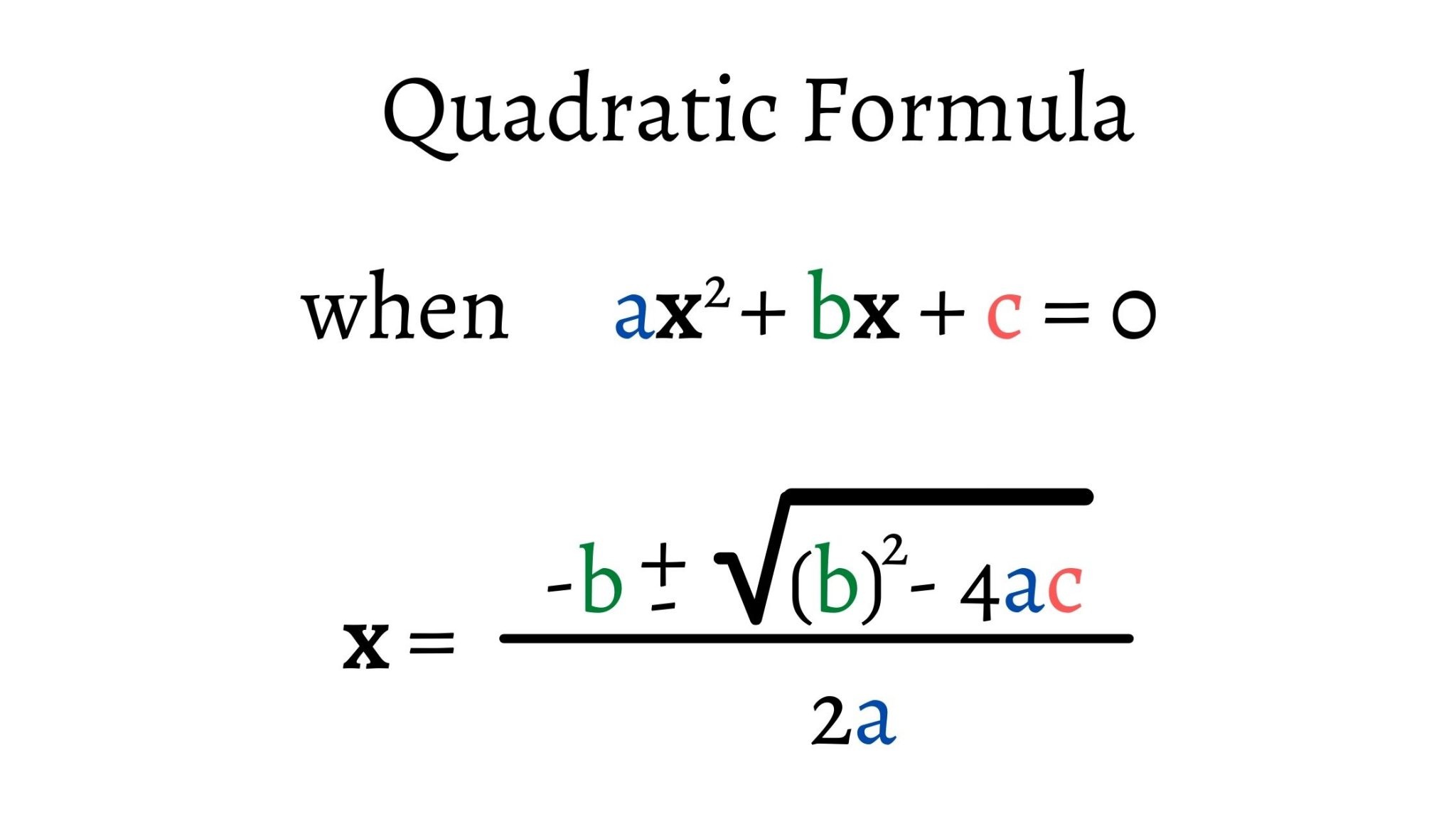
We can determine the nature of the roots by using the discriminant. But for finding the nature of the roots, we don't actually need to solve the equation. and so we can say that the equation has two real and different roots. two real and equal roots (it means only one real root)įor example, in the above example, the roots of the quadratic equation x 2 - 7x + 10 = 0 are x = 2 and x = 5, where both 2 and 5 are two different real numbers.The nature of the roots of a quadratic equation talks about "how many roots the equation has?" and "what type of roots the equation has?". So the best methods that always work for finding the roots are quadratic formula and completing the square methods. Note that the factoring method works only when the quadratic equation is factorable and we cannot find the complex roots of the quadratic equation using the graphing method. We can observe that the roots of the quadratic equation x 2 - 7x + 10 = 0 are x = 2 and x = 5 in each of the methods. Therefore, the roots of the quadratic equation are x = 2 and x = 5. Identify the x-intercepts which are nothing but the roots of the quadratic equation.Graph the left side part (the quadratic function) either manually or using the graphing display calculator (GDC).Solve by taking square root on both sides.įinding Roots of Quadratic Equation by Graphing.X = / (2(1))įinding Roots of Quadratic Equation by Completing Square Substitute them in the quadratic formula and simplify.Find a, b, and c values by comparing the given equation with ax 2 + bx + c = 0.Set each of these factors to zero and solve.įinding Roots of Quadratic Equation by Quadratic Formula.Finding Roots of Quadratic Equation by Factoring Note that In each of these methods, the equation should be in the standard form ax 2 + bx + c = 0.

Let us discuss each of these methods here by solving an example of finding the roots of the quadratic equation x 2 - 7x + 10 = 0 (which was mentioned in the previous section) in each case. To know about these methods in detail, click here.
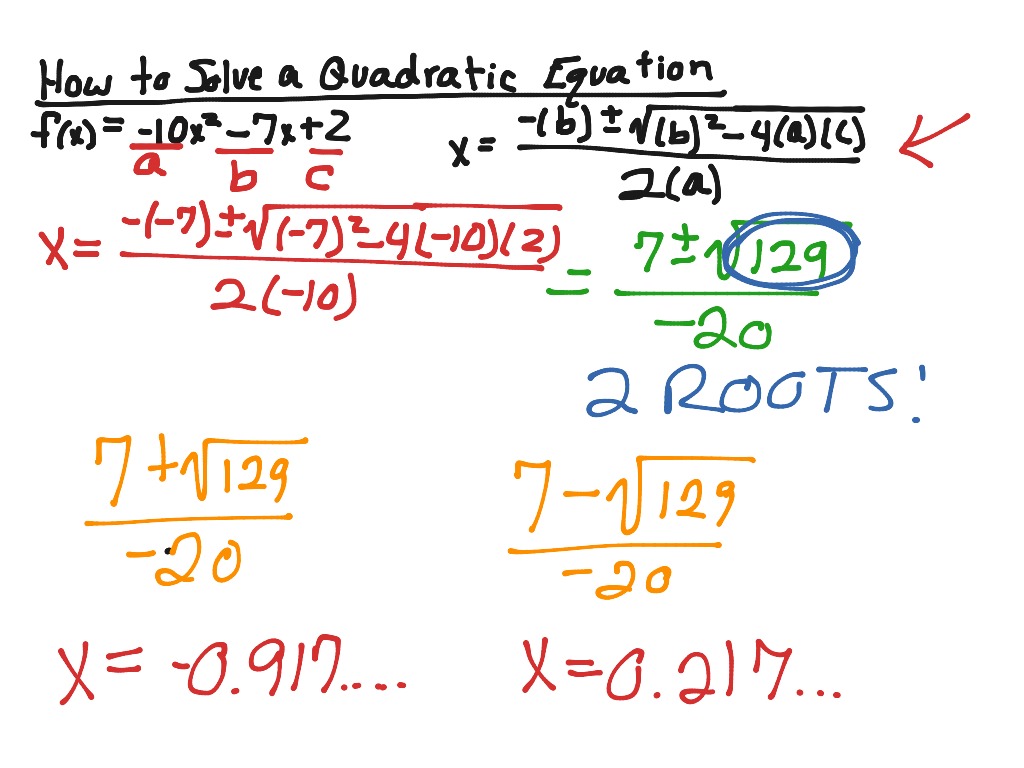
Along with this method, we have several other methods to find the roots of a quadratic equation. In the previous section, we have seen that the roots of a quadratic equation can be found using the quadratic formula. The process of finding the roots of the quadratic equations is known as "solving quadratic equations".
#Quadratic equations how to#
How to Find the Roots of Quadratic Equation? This is known as the quadratic formula and it can be used to find any type of roots of a quadratic equation.


 0 kommentar(er)
0 kommentar(er)
